A-1 Trap
分数 20
A robot is designed to move on a map from South toward North. When some obstacle is encountered, the robot can only turn toward West and moves until it can turn toward North and continue.
Given a squared map with n×n blocks, a robot can start from any position below the bottom line (South) and its target is to reach the top line (North). (By the way, kindly remind you that the left-hand-side of the map is West and the right-hand-side is East.)
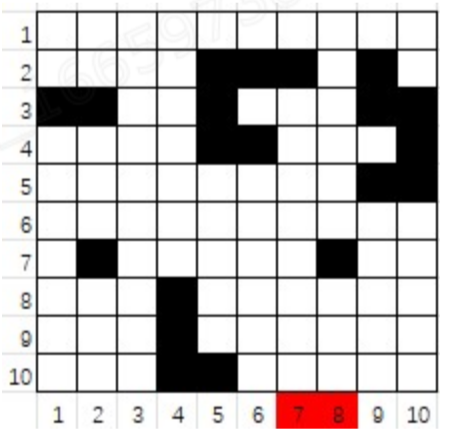
If some obstacles are placed in the map, the robot might get trapped if it starts from certain positions and can never reach the North line. For example, in the situation given by the following figure, the robot will be trapped if it starts from either position 7 or 8.
Your job is to point out those starting positions which will get the robot trapped.
Note: it is assumed that a robot can move out of the map boundary, and all the blocks around the map are open, without any obstacle. Hence if the robot starts from any position out of the West or East boundary, it can certainly reach North without any problem. Therefore we only have to consider the positions between the West and East boundaries (e.g. the positions from 1 to 10 below the South line in the above figure). Besides, as long as the robot can reach the North line, it is considered successful even of it ends up at out of the boundary (e.g. the robot will have to move out of the map if starts from either the positions 1 or 2, but it can still reach the North line).
Input Specification:
Each input file contains one test case. Each case starts from a positive integer n (≤100) in a line, which is the size of the map. Then n lines follow, each contains n characters, which are either 0 for an open block, or 1 for a block with obstacle. The first line corresponds to the North boundary and the last line the South.
Output Specification:
Output in a line all the starting positions which can get the robot trapped, in increasing order. The positions are indexed from West to East, starting from 1. It is guaranteed that there is at least one output.
All the numbers must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.
Sample Input:
10
0000000000
0000111010
1100100011
0000110001
0000000011
0000000000
0100000100
0001000000
0001000000
0001100000Sample Output:7 8
题意:给个正方形的长为n的网格图,从第n+1行出发,能往北走往北走,不能往北走就往西走,直到能往北走为止。求从哪几列出发能到达第1行。网格图外所有地方可以到达。
标签:模拟
解析:难点在于题目很绕,不太好懂。由于只有往上往左两种走法,因此超出边界只可能是超出左边界,而一旦超出左边界,一定能到达最北端。所以一旦到达第一列即可返回true。
#include <bits/stdc++.h>
using namespace std;
bool f(const vector<string>& g, int i, int j, int n) {
if (i == 0 || j == 0) return 1;
if (g[i-1][j] == '0') return f(g, i-1, j, n);
else if (g[i][j-1] == '0') return f(g, i, j-1, n);
return 0;
}
int main() {
int n;
cin >> n;
vector<string> g(n+1, string(n, '0'));
for (int i = 0; i < n; ++i) {
cin >> g[i];
}
bool b = 0;
for (int j = 0; j < n; ++j) {
if (!f(g, n, j, n)) {
if (b == 1) cout<<' ';
cout<<j+1;
b=1;
}
}
return 0;
}A-2 Queue Using Two Stacks
分数 25
A queue (FIFO structure) can be implemented by two stacks (LIFO structure) in the following way:
Start from two empty stacks s1 and s2
When element e is enqueued, it is actually pushed onto s1
When we are supposed to dequeue, s2 is checked first. If s2 is empty, everything in s1 will be transferred to s2 by popping from s1 and immediately pushing onto s2. Then we just pop from s
2 -- the top element of s2 must be the first one to enter s1, thus is the first element that was enqueued.
Assume that each operation of push or pop takes 1 unit of time. You job is to tell the time taken for each dequeue.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10^3 ), which are the number of operations. Then N lines follow, each gives an operation in the format
Operation Element
where Operation being I represents enqueue and O represents dequeue. For each I, Element is a positive integer that is no more than 10^6. No Element is given for O operations.
It is guaranteed that there is at least one O operation.
Output Specification:
For each dequeue operation, print in a line the dequeued element and the unites of time taken to do this dequeue. The numbers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.
In case that the queue is empty when dequeue is called, output in a line ERROR instead.
Sample Input:
10
I 20
I 32
O
I 11
O
O
O
I 100
I 66
OSample Output:
20 5
32 1
11 3
ERROR
100 5题意:两个栈实现队列,并统计操作数。具体操作题目已给出。入队即push给s1,出队先检查s2是不是空,不是的话s2直接pop,是的话s1中元素一pop后马上push给s2,到s1为空为止,然后s2再pop。
标签:栈,队列
解析:模拟即可。
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
stack<int> s1, s2;
for (int i = 0; i < n; ++i) {
char op;
cin >> op;
if (op == 'I') {
int ele;
cin >> ele;
s1.push(ele);
} else {
if (s1.empty() && s2.empty()) cout<<"ERROR";
else {
if (!s2.empty()) {
cout << s2.top() << ' ' << "1";
s2.pop();
} else {
int cnt = s1.size() * 2 + 1;
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
cout << s2.top()<< ' ' << cnt;
s2.pop();
}
}
if (i != n-1) cout<<endl;
}
}
return 0;
}A-3 Rank of Binary Tree
分数 25
Here we define the rank of a binary tree as n1×n2 /n0 where ni is the number of nodes of degree i for i=0,1,2.
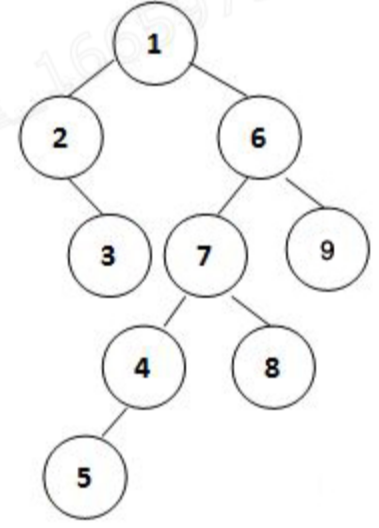
For example, given a tree shown by the figure, its rank is 2×3/4=1.5.
Given the inorder and preorder traversal sequences of a binary tree, you are supposed to calculate its rank.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤20), which is the total number of nodes in the tree. Then given in the following 2 lines are the inorder and preorder traversal sequences of the tree, respectively. All the keys in the tree are distinct positive integers in the range of int.
Output Specification:
For each case, print in a line the way we calculate the rank, and the integer part of the rank. The format is:
n1 * n2 / n0 = rank
Sample Input:
9
2 3 1 5 4 7 8 6 9
1 2 3 6 7 4 5 8 9Sample Output:2 * 3 / 4 = 1
题意:由前序和中序遍历构造二叉树,然后统计有1个孩子,2个孩子,0个孩子的节点有几个,按要求输出。
标签:二叉树,前序遍历,中序遍历
解析:由遍历构造树PAT不是第一次考了。这题思路是前序遍历中第一个节点必为根节点,在中序遍历中找到这一节点,其中序遍历数组左侧必为左子树,右侧必为右子树。对于左子树和右子树,可以用同样的方法处理,直到只有1个节点或节点为空,这就变成一个递归问题。事实上这是经典数据结构题,各大算法网站上都有,同类型题也能方便地找到,贴一个力扣的:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
统计孩子遍历一遍树即可。
#include <bits/stdc++.h>
using namespace std;
int n0 = 0, n1 = 0, n2 = 0;
unordered_map<int, int> idx;
vector<int> in, pre;
struct Node {
Node *left, *right;
int val;
Node(int v){val = v;}
};
Node* buildTree(int pl, int pr, int il, int ir) {
if (pl > pr) return nullptr;
int proot = pl;
int iroot = idx[pre[proot]];
Node* root = new Node(pre[proot]);
int slt = iroot - il;//size of left subtree
root->left = buildTree(pl+1, pl+slt, il, iroot-1);
root->right = buildTree(pl+slt+1, pr, iroot+1, ir);
return root;
}
void nCounter(Node* node) {
if (!node) return;
if (!node->left && !node->right) {
++n0;
return;
}
nCounter(node->left);
nCounter(node->right);
if (node->left) {
if (node->right) {
++n2;
} else {++n1;}
} else if (node->right) {
++n1;
}
}
int main() {
int n;
cin >> n;
in.resize(n); pre.resize(n);
for (int i = 0; i < n; ++i) cin >> in[i];
for (int i = 0; i < n; ++i) cin >> pre[i];
for (int i = 0; i < n; ++i) idx[in[i]] = i;
auto root = buildTree(0, n-1, 0, n-1);
nCounter(root);
printf("%d * %d / %d = %d", n1, n2, n0, n1*n2/n0);
return 0;
}A-4 Big Number
分数 30
How to generate a big number of N digits randomly? One way is to find N kids, give each one a card with one's index written on one side (hence it is assumed that the kids are indexed from 1 to N), and ask them to write down a 1-digit number randomly on the other side. Then let the kids pin their digits in a line, on the wall, one by one in ascending order of their indices.
However, it's very difficult to let hundreds of thousands of kids to follow the order. The result is that we have cards pinned randomly all over the wall, some even show the wrong sides. For example, if the 23rd kid has written down 8, we are supposed to find the number 8 on the wall. But instead we might find 23... Your job is to rearrange these cards so that we can obtain the big number as required.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10^5). Then N lines follow, each describes a card in the format n1 n2 where the two numbers are the numbers written on the two sides of a card.
Output Specification:
For each test case, print in a line the N-digit number as required. That is, print the digits written by the kids in ascending order of their indices. In case that there are 1-digit numbers written on both sides, it would be hard to tell which one is the index and which one is the number written by the kid. Hence the solution may not be unique. In this case, just output the smallest resulting number.
It is guaranteed that a solution exists.
Sample Input:
12
7 11
8 9
3 1
2 12
4 6
10 0
5 1
2 5
6 8
1 4
7 2
9 3Sample Output:359114268072
题意:有N组数,每组数有2个数,可能是下标也可能是数值(数值只能是0~9中一个),输出由这N组数表示的最小N位数。
标签:贪心,深度优先搜索dfs
解析:显然,对于一组数,只要出现2位以上的数,它就必定表示这一组数的数位,那么另一个数就是这一位的数值。因此,出现不同情况的只可能是下标为1到9的9组数。数据规模很小,所以算法的时间复杂度可以很奢侈。在这里我使用贪心,对每组的两个数哪个是下标哪个是数值,既然不知道,那就都试试。怎么试?建立数组tv存这9组数,借助dfs从1到9逐渐完善tv。每试完一组,用集合cap来记住这一组的信息已经用掉了,把它erase掉,用完的信息存入tv,进入下一层dfs。考试过程中看到27,28,29分的同学都有,这里给出我试出来的一个排查用例:
2
1 2
1 2有个1分用例是两组中元素相同,如果输入时没有都记下来就会丢掉这1分。
对于另一个2分的用例,可能是数据并没有10个以上,所以对10个以下的数据输出和dfs时做一些处理即可。
还有前导0可能也有测试点,因为题目要求确切的n位数,所以不能有前导0.
#include <bits/stdc++.h>
using namespace std;
int n;
void dfs(int cur, vector<int>& tv, vector<int>& res, set<pair<int,int>>& cap) {
//printf("\ndfs:cur=%d", cur);
if (cur == 10 || cur > n) {
res = min(res, tv);
return;
}
for (int i = 0; i < 10; ++i) {
if (cur==1&&i==0) continue;
if (cap.count({cur, i})) {
cap.erase({cur, i});
tv[cur] = i;
dfs(cur+1, tv, res, cap);
cap.emplace(cur, i);
}
if (cap.count({i, cur})) {
cap.erase({i, cur});
tv[cur] = i;
dfs(cur+1, tv, res, cap);
cap.emplace(i, cur);
}
}
}
int main() {
cin >> n;
set<pair<int,int>> cap;
vector<int> v(n+1);//storage: index >= 10
for (int i = 0; i < n; ++i) {
int a, b;
cin >> a >> b;
if (a >= 10) {
v[a] = b;
} else if (b >= 10) {
v[b] = a;
} else {
if (cap.count({a, b})) cap.emplace(b, a);
else cap.emplace(a, b);
}
}
vector<int> res(10, 0x3f3f3f3f);
vector<int> tv(10, 0x3f3f3f3f);//temp vector
dfs(1, tv, res, cap);
for (int i = 1; i < 10 && i <= n; ++i) {
cout<<res[i];
}
for (int i = 10; i <= n; ++i) cout<<v[i];
return 0;
}一点想说的话:我个人也是非常的菜,这是我第4次考PAT了,前3次不仅都没到60,而且还越考越低orz。PAT我完全是靠运气在考,因为出题人默认你知道数据结构和算法的一些知识点,比如前中后序遍历顺序,快速排序如何实现等等。此外,我还因为题目关键处出现生词寄过,也经常出现读题不仔细,做了一大半发现题读错了全部重来等等等等的问题。前3次的失败也是真的很难受,本来我就在很早之前就试过真题1小时全ac了,一直都是发挥不出来。而且题目分值很大,基本上一个读不懂,一个读错题,或者涉及到不会的知识点,那就是几十分几十分的掉,就算我自认为有8,90分水准,实际上打出来却总是4,50分的成绩。当然,这次运气真的很好,题目简单,而且恰好我都会。第一题读懂就很简单(不过读懂也是真不容易,我做了20来分钟还没拿满分,直接跳了,后面回来再看题才发现往西走不是到底的,而是一次一步),第二题更是啥都告诉你了照做就行,第三题leetcode原题做过(之前PAT也刚考过类似的,那次是中序和后序构建二叉树),第四题恰好是我最擅长的dfs,贪心那一步卡了思路,最后开考2小时达到97分时不会debug但是随手编了几个样例刚好发现了问题。最终离收卷还剩15分钟的时候达到了满分。还是很意外的吧,毕竟前面考那么烂,这次完全一点积极性也没有了,报名都是卡着截止前一天才报的,想着考6,70不错了,居然干满了,真的非常意外。不过这次心态也真有点不一样,开考前就感觉自己状态真的很好,也早早准备好了考场环境,带着数据结构的书重点看了看基础知识,重点备战了dijkstra算法(虽然完全没考)。开考后第一题有点绕,其实有点慌的,不过卡很久跳过以后看到2,3题,那真是狂喜,一看就知道我肯定会,起码能60分保底了。最后一题倒是一开始就想到10位以后不用管了,但是贪心思路有误,等纠正过来写出能拿部分样例的代码时已经剩下不到半小时了。当时心里就告诉自己一定要冷静,满分还是很有机会的,然后debug15分钟,最终是搞定了。实时排名大概看了几次,全程都是保持在20多30名,除了最后一题写出第一份代码前到了50名左右,但是写出以后又是27左右了。再然后,一发ac,噢!好兴奋,第一耶~开心地截了个图,
然后复制一下题目,准备写写题解了。最后剩下的15分钟,没有直接退出考场,而是享受了一下胜利的喜悦,哈哈哈哈。真的很开心,不过可能也是太紧张了,考完以后傻了一天一夜,啥也没动力。
几次考下来还对出题方向有点心得,pat最近考试的思路和甲级题集前几十道还是不太一样,第2,3题像图书管理系统那种设计struct的题型变少了几乎没考过(一般在中间两题),树很喜欢考几乎从不缺席(一般不在第一题),最短路径也常考但比树少(一般在后两题),纯coding的模拟题每次必有(一般在前两题)。第一题一般是模拟,字符串或者最小公因数之类简单算法。二三题一般是经典数据结构。第四题上难度的方式就3种,一种是上图相关题拉起代码量;一种是类似这次考考思维,想明白就很简单;一种是考点高级些的数据结构,比如平衡BST,并查集。
最后,给还在努力刷甲级的朋友们两个推荐:
PAT甲级题【真题】全讲解 (Advanced Level) Practice_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1Mt4y197kC
GitHub - liuchuo/PAT:
https://github.com/liuchuo/PAT